7 - La luminance V(λ) selon la CIE

 La CIE propose une fonction appelée "efficacité lumineuse spectrale relative"  qui tient compte de la luminosité spectrale des couleurs.


Comprendre la fonction d'efficacité lumineuse spectrale relative vous sera indispensable pour comprendre, plus loin, le principe du modèle CIE-1931. Nous allons voir comment cette fonction peut être assimilée à la luminance (à une constante près).

La luminance est la correspondance dans le domaine physique de la sensation visuelle qu’on nomme clarté.  Ces deux grandeurs décrivent exactement la même chose, mais sur une échelle différente.
En notation française on distincte la luminance lumineuse (ou visuelle) de la luminance énergétique, appelée radiance en anglais. Nous nous intéressons ici à la luminance lumineuse.

Lorsque la CIE crée en 1931 les modèles CIE RGB et CIE XYZ, elle y associe une luminance dérivée de la fonction d'efficacité lumineuse spectrale relative crée en 1924. A cette époque on nommait cette fonction plus simplement facteur de visibilité V(λ).

Cette formulation d'une nouvelle luminance est le point central vers la modélisation du modèle CIE-RGB/CIE-XYZ 1931.

Lrgb  = V(λ)       (6.1)

Luminance dans le RGB  = efficacité lumineuse spectrale relative

Concrètement, cette équation veut dire qu'on peut simuler avec un système RGB, la luminance d'une couleur spectrale dont le niveau d'efficacité spectrale est fonction de λ.

Pour comprendre dans les articles suivants, la modélisation du modèle CIE-1931, voici un petit résumé sur l’historique et l’avènement de cette fonction V(λ).

1 - Le flux lumineux et le lumen

En 1907, Perley Nutting cherche à déterminer le lien entre le flux énergétique des ondes électromagnétiques et leurs sensations visuelles. Ce lien est la grandeur qu'on appelle aujourd'hui le flux lumineux.  Il définit ce flux dans son facteur de "Visibilité" V(λ). Le flux lumineux n’a pas encore d’unité définie à cette époque. Il donne alors le nom de lumen à cette grandeur sans déterminer précisément sa valeur.

Fig. 1. La lumière ne représente qu'une portion infime des ondes électromagnétiques. Le fait qu'elle soit visible n'est pas dû à une propriété physique de cette zone, mais à une capacité sensorielle de l'espèce humaine.

2 - La fonction d'efficacité lumineuse spectrale

En 1923, Gibson et Tyndall supervisent un nouveau projet sous le nom de Visibility of radiant energy afin de donner une valeur précise au lumen. Deux études sont menées en parallèle. Une pour la vision de jour appelée fonction d’efficacité photopique et une autre pour la vision nocturne appelée fonction d’efficacité scotopique. Notons que le modèle CIE 1931 ne s’appuie que la fonction basée sur la lumière du jour. Leurs travaux sont entérinés par la CIE en 1924 avec l’adoption du standard
CIE-1924 V(λ).

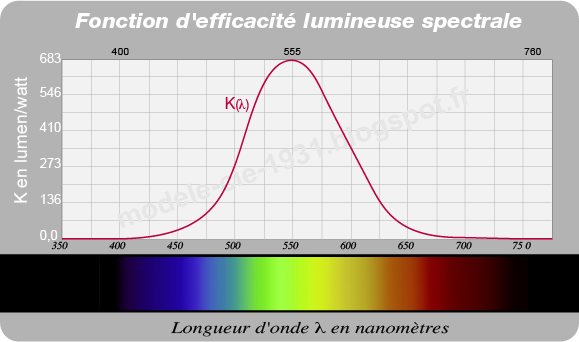Fig. 2. La fonction d’efficacité lumineuse fait le lien entre flux lumineux et flux énergétique d’une radiation. Elle varie toujours entre 0 et 683 lumens/watt. C’est une grandeur physique objective.

Un rayonnement lumineux d’une puissance de x watts n'est pas perçu avec la même intensité lumineuse selon la teinte de la couleur. On appelle efficacité lumineuse ce niveau de perception et elle s’exprime en lumen/watt. L’efficacité lumineuse exprime la pondération apportée par la longueur d’onde d’un rayonnement.

L’efficacité lumineuse est notée K, elle est fonction de la longueur d’onde notée (λ). C’est le rapport entre le flux lumineux F et le flux énergétique P

3 - La fonction d'efficacité lumineuse spectrale relative

La fonction d'efficacité lumineuse spectrale K est liée à une grandeur physique (évaluée en watt) qui lui donne une dimension physique objective, indépendante de la vision humaine. Il est possible de couper ce lien avec le monde physique, et avoir une fonction liée avec la vision humaine. C'est ce que propose l’efficacité lumineuse spectrale relative qui est notée V(λ).

Fig. 3. Diagramme de plusieurs ensembles de données qui décrivent la fonction de visibilité relative.  D'après le recueil des travaux de la 16e rencontre de la Commision internationale de l'Eclairage à Genève en 1934

C'est une moyenne des données de la figure 3 qui va être retenue pour être collectée dans la table de la figure 4 [1].

Fig. 4. Entête de la table originale de 1924 ne comporte que 37 mesures. Les pas vont de 10 en 10 nm et donc on ne voit pas apparaitre le maximum égal à 1 situé à 555 nm. Les valeurs intermédiaires seront calculées par interpolation.

Les données du tableau de la figure 4 sont plus perceptibles sous forme de graphique telles que représentées sur la figure 5.

Fig. 5. La fonction d’efficacité lumineuse spectrale relative se développe entre les valeurs 0 et 1.
Elle n’est plus directement reliée à la puissance énergétique.

On passe de l’efficacité lumineuse spectrale K(λ) à l’efficacité lumineuse spectrale relative V(λ) en donnant la valeur 1 à l'efficacité maximum. Cette échelle devenue relative supprime le lien avec la puissance en watt et on obtient une nouvelle grandeur uniquement subjective, c’est-à-dire uniquement liée à la sensibilité spectrale de l’oeil. V(λ) est une grandeur subjective sans dimension.

Puis par déduction, on obtient le flux lumineux exprimé en lumen :

F = 683 P V(λ)       (6.4)

C’est lors de ces travaux qu’a été donnée une valeur définitive au lumen. En effet, selon l’équation précédente, lorsque la fonction V(λ) prend la valeur 1, c'est-à-dire avec la couleur [555 nm], on voit que 1 lumen est produit par 1/683 Watt [2]. Cette valeur du lumen est historiquement le fondement de l’ensemble des grandeurs de la photométrie. La candela, unité de l’intensité lumineuse, a donc été déduite du lumen. Aujourd’hui, la candela occupe la place d’unité de référence de la photométrie et donc on raisonne de manière inverse en définissant le lumen depuis la candela.

4 - RGB et fonction V(λ)

Imaginez maintenant qu'on veuille utiliser cette fonction V(λ) dans un espace colorimétrique en tant que luminosité. Il faudrait qu'on se débarrasse du facteur 683 P. Pour cela, il suffit que l'ensemble des couleurs réalisables soient de radiance identique. On a donc :

F = k V(λ)

ou

Lrgb  =  k V(λ)

A une constante près, un modèle RGB peut simuler la luminance de la fonction V. C'est cette possibilité qui va utilisée pour la construction du modèle CIE-RGB 1931.


Notes

[1] Les relevés de la première table ont été faits entre 380 nm et 760 nm (voir fig 4). Aujourd’hui on situe les limites de visibilité entre 360 nm et 830 nm.

[2] Les étudiants qui ont du mal à retenir la définition officielle du lumen, se consoleront en sachant qu'il en existe une beaucoup plus simple.